Research
My main interest lies in the area of statistical signal and image understanding with a focus on theoretical issues. This research area has also been called computational vision since one seeks to design computerized systems for understanding scenes from camera images, much like our own human vision system. There is a strong need for such tools in medical diagnostics, face recognition, video surveillance, undersea imaging, terrain mapping, and satellite image analysis. In military domain, the problem of battlefield target recognition continues to motivate newer research which is a vast importance
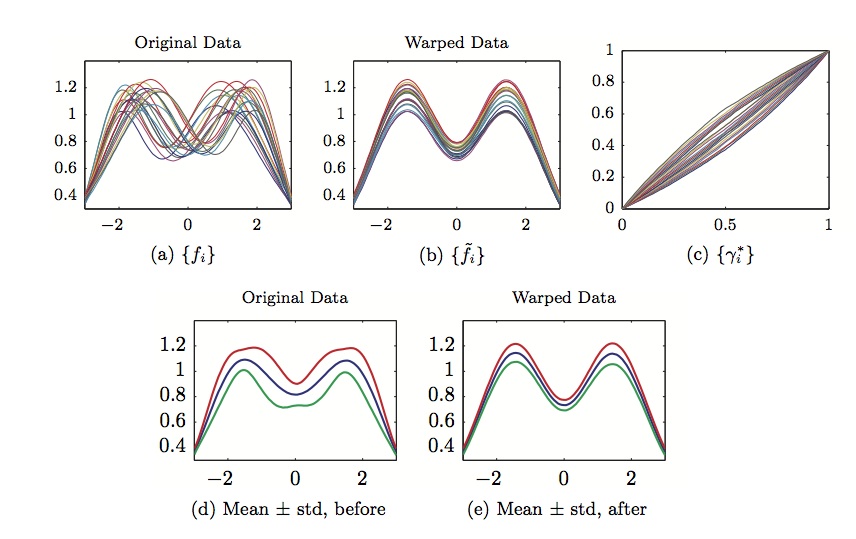
My current focus is in the area of functional data analysis the focus on the registration and statistical analysis functions in \mathbb{R}^n and images. Specifically, looking at uncertainty quantification and regression modeling of this type of data. Small changes in the sensor placement introduce compositional noise in this type of data. The traditional alignment techniques are based on energy functions that are not proper distances, and necessitate a separate (and thus suboptimal) choice of distance to compare the aligned functions. I work on methods that present a comprehensive technique, for removing compositional noise and aligning functions, that: (1) uses a single cost function for data alignment, (2) combines the data and smoothness in natural fashion, and (3) leads to a proper distance between aligned functions. It is based on establishing re-parameterization orbits of functions under the warping group and defining a distance between orbits using the Fisher-Rao metric. Using this metric we can compute a proper covariance and perform functional principal component analysis. From the principal components we can develop models of the y variability (aligned data) and x variability (warping functions) and perform classification. I have investigated the use of this framework in modeling and classification of spectral signatures in acoustic data, image registration and classification, and tolerance bound generation.
Sandia Statistical Sciences
FSU Statistical Shape and Modeling Group